statistics | Richard David Feinman

Posts Tagged ‘statistics’

Red meat and cancer

Posted: November 10, 2015 in Cancer, Epidemiology, Evidence Based Medicine, misuse of statistics, Observational Studies, Red Meat
Tags: Cancer, hazard ratio, Meat Intake and Mortality, red meat,, statistics

As the nutrition world implodes, there are a lot of accusations about ulterior motives and personal gain. (A little odd, that in this period of unbelievable greed — CEO’s ripping off public companies for hundreds of millions of dollars, congress trying to give tax breaks to billionaires — book authors are upbraided for trying to make money). So let me declare that I am not embarrassed to be an author for the money — although the profits from my book do go to research, it is my own research and the research of my colleagues. So beyond general excellence (not yet reviewed by David Katz), I think “World Turned Upside Down” does give you some scientific information about red meat and cancer that you can’t get from the WHO report on the subject.

The WHO report has not yet released the evidence to support their claim that red meat will give you cancer but it is worth going back to one of the previous attacks. Chapters 18 and 19 discussed a paper by Sinha et al, entitled “Meat Intake and Mortality.” The Abstract says “Conclusion: Red and processed meat intakes were associated with modest increases in total mortality, cancer mortality, and cardiovascular disease mortality,” I had previously written a blogpost about the study indicating how weak the association was. In that post, I had used the data on men but when I incorporated the information into the book, I went back to Sinha’s paper and analyzed the original data. For some reason, I also checked the data on women. That turned out to be pretty surprising:

Sinha_Table3_Chapter18_Apr22

I described on Page 286: “The population was again broken up into five groups or quintiles. The lower numbered quintiles are for the lowest consumption of red meat. Looking at all cause mortality, there were 5,314 deaths [in lowest quintile] and when you go up to quintile 05, highest red meat consumption, there are 3,752 deaths. What? The more red meat, the lower the death rate? Isn’t that the opposite of the conclusion of the paper? And the next line has [calculated] relative risk which now goes the other way: higher risk with higher meat consumption. What’s going on? As near as one can guess, “correcting” for the confounders changed the direction….” They do not show most of the data or calculations but I take this to be equivalent to a multivariate analysis, that is, red meat + other things gives you risk. If they had broken up the population by quintiles of smoking, you would see that that was the real contributor. That’s how I interpreted it but, in any case, their conclusion is about meat and it is opposite to what the data say.

So how much do you gain from eating red meat? “A useful way to look at this data is from the standpoint of conditional probability. We ask: what is the probability of dying in this experiment if you are a big meat‑eater? The answer is simply the number of people who both died during the experiment and were big meat‑eaters …. = 0.0839 or about 8%. If you are not a big meat‑eater, your risk is …. = 0.109 or about 11%.” Absolute gain is only 3 %. But that’s good enough for me.

Me, at Jubilat, the Polish butcher in the neighborhood: “The Boczak Wedzony (smoked bacon). I’ll take the whole piece.”

Wedzony_Nov_8

Boczak Wedzony from Jubilat Provisions.

Rashmi Sinha is a Senior Investigator and Deputy Branch Chief and Senior at the NIH. She is a member of the WHO panel, the one who says red meat will give you cancer (although they don’t say “if you have the right confounders.”)

So, buy my book: Amazon, Alibris, or

Direct: Personalized, autographed copy $ 20.00 free shipping USA only. Use coupon code: SEPT16

Observations Generate hypotheses. Observational Studies Test Hypotheses. Association Implies Causality (Sometimes).

Posted: June 12, 2013 in Association and Causality, Crisis in Nutrition, Epidemiology, Evidence Based Medicine, misuse of statistics, Observational Studies, Red Meat
Tags: association and causality, Bradford Hill, epidemiology, red meat, statistics

“…789 deaths were reported in Doll and Hill’s original cohort. Thirty-six of these were attributed to lung cancer. When these lung cancer deaths were counted in smokers versus non-smokers, the correlation virtually sprang out: all thirty-six of the deaths had occurred in smokers. The difference between the two groups was so significant that Doll and Hill did not even need to apply complex statistical metrics to discern it. The trial designed to bring the most rigorous statistical analysis to the cause of lung cancer barely required elementary mathematics to prove his point.”

Siddhartha Mukherjee —The Emperor of All Maladies.

Scientists don’t like philosophy of science. It is not just that pompous phrases like hypothetico-deductive systems are such a turn-off but that we rarely recognize it as what we actually do. In the end, there is no definition of science and it is hard to generalize about actual scientific behavior. It’s a human activity and precisely because it puts a premium on creativity, it defies categorization. As the physicist Steven Weinberg put it, echoing Justice Stewart on pornography:

“There is no logical formula that establishes a sharp dividing line between a beautiful explanatory theory and a mere list of data, but we know the difference when we see it — we demand a simplicity and rigidity in our principles before we are willing to take them seriously [1].”

A frequently stated principle is that “observational studies only generate hypotheses.” The related idea that “association does not imply causality” is also common, usually cited by those authors who want you to believe that the association that they found does imply causality. These ideas are not right or, at least, they insufficiently recognize that scientific experiments are not so easily wedged into categories like “observational studies.” The principles are also invoked by bloggers and critics to discredit the continuing stream of observational studies that make an association between their favorite targets, eggs, red meat, sugar-sweetened soda and a metabolic disease or cancer. In most cases, the studies are getting what they deserve but the bills of indictment are not quite right. It is usually not simply that they are observational studies but rather that they are bad observational studies and, in any case, the associations are so weak that it is reasonable to say that they are an argument for a lack of causality. On the assumption that good experimental practice and interpretation can be even roughly defined, let me offer principles that I think are a better representation, insofar as we can make any generalization, of what actually goes on in science:

Observations generate hypotheses.

Observational studies test hypotheses.

Associations do not necessarily imply causality.

In some sense, all science is associations.

Only mathematics is axiomatic.

If you notice that kids who eat a lot of candy seem to be fat, or even if you notice that candy makes you yourself fat, that is an observation. From this observation, you might come up with the hypothesis that sugar causes obesity. A test of your hypothesis would be to see if there is an association between sugar consumption and incidence of obesity. There are various ways — the simplest epidemiologic approach is simply to compare the history of the eating behavior of individuals (insofar as you can get it) with how fat they are. When you do this comparison you are testing your hypothesis. There are an infinite number of things that you could have measured as an independent variable, meat, TV hours, distance from the French bakery but you have a hypothesis that it was candy. Mike Eades described falling asleep as a child by trying to think of everything in the world. You just can’t test them all. As Einstein put it “your theory determines the measurement you make.”

Associations predict causality. Hypotheses generate observational studies, not the other way around.

In fact, association can be strong evidence for causation and frequently provide support for, if not absolute proof, of the idea to be tested. A correct statement is that association does not necessarily imply causation. In some sense, all science is observation and association. Even thermodynamics, that most mathematical and absolute of sciences, rests on observation. As soon as somebody observes two systems in thermal equilibrium with a third but not with each other (zeroth law), the jig is up. When somebody builds a perpetual motion machine, that’s it. It’s all over.

Biological mechanisms, or perhaps any scientific theory, are never proved. By analogy with a court of law, you cannot be found innocent, only not guilty. That is why excluding a theory is stronger than showing consistency. The grand epidemiological study of macronutrient intake vs diabetes and obesity shows that increasing carbohydrate is associated with increased calories even under conditions where fruits and vegetables also went up and fat, if anything went down. It is an observational study but it is strong because it gives support to a lack of causal effect of increased carbohydrate and decreased fat on outcome. The failure of total or saturated fat to have any benefit is the kicker here. It is now clear that prospective experiments have, in the past, and will continue to show, the same negative outcome. Of course, in a court of law, if you are found not guilty of child abuse, people may still not let you move into their neighborhood. It is that saturated fat should never have been indicted in the first place.

An association will tell you about causality 1) if the association is strong and 2) if there is a plausible underlying mechanism and 3) if there is no more plausible explanation — for example, countries with a lot of TV sets have modern life styles that may predispose to cardiovascular disease; TV does not cause CVD.

Re-inventing the wheel. Bradford Hill and the history of epidemiology.

Everything written above is true enough or, at least, it seemed that way to me. I thought of it as an obvious description of what everybody knows. The change to saying that “association does not necessarily imply causation” is important but not that big a deal. It is common sense or logic and I had made it into a short list of principles. It was a blogpost of reasonable length. I described it to my colleague Gene Fine. His response was “aren’t you re-inventing the wheel?” Bradford Hill, he explained, pretty much the inventor of modern epidemiology, had already established these and a couple of other principles. Gene cited The Emperor of All Maladies, an outstanding book on the history of cancer. I had read The Emperor of All Maladies on his recommendation and I remembered Bradford Hill and the description of the evolution of the ideas of epidemiology, population studies and random controlled trials. I also had a vague memory, of reading the story in James LeFanu’s The Rise and Fall of Modern Medicine, another captivating history of medicine. However, I had not really absorbed these as principles. Perhaps we’re just used to it, but saying that an association implies causality only if it is a strong association is not exactly a scientific breakthrough. It seems an obvious thing that you might say over coffee or in response to somebody’s blog. It all reminded me of learning, in grade school, that the Earl of Sandwich had invented the sandwich and thinking “this is an invention?” Woody Allen thought the same thing and wrote the history of the sandwich and the Earl’s early failures — “In 1741, he places bread on bread with turkey on top. This fails. In 1745, he exhibits bread with turkey on either side. Everyone rejects this except David Hume.”

At any moment in history our background knowledge — and accepted methodology — may be limited. Some problems seem to have simple solutions. But simple ideas are not always accepted. The concept of the random controlled trial (RCT), obvious to us now, was hard won and, proving that any particular environmental factor — diet, smoking, pollution or toxic chemicals was the cause of a disease and that, by reducing that factor, the disease could be prevented, turned out to be a very hard sell, especially to physicians whose view of disease may have been strongly colored by the idea of an infective agent.

The Rise and Fall of Modern Medicine describes Bradford Hill’s two demonstrations that streptomycin in combination with PAS (para-aminosalicylic acid) could cure tuberculosis and that tobacco causes lung cancer as one of the Ten Definitive Moments in the history of modern medicine (others shown in the textbox). Hill was Professor of Medical Statistics at the London School of Hygiene and Tropical Medicine but was not formally trained in statistics and, like many of us, thought of proper statistics as common sense. An early near fatal case of tuberculosis also prevented formal medical education. His first monumental accomplishment was, ironically, to demonstrate how tuberculosis could be cured with the combination of streptomycin and PAS. In 1941, Hill and co-worker Richard Doll undertook a systematic investigation of the risk factors for lung cancer. His eventual success was accompanied by a description of the principles that allow you to say when association can be taken as causation.

Ten Definitive Moments from Rise and Fall of Modern Medicine.

1941: Penicillin

1949: Cortisone

1950: streptomycin, smoking and Sir Austin Bradford Hill

1952: chlorpromazine and the revolution in psychiatry

1955: open-heart surgery – the last frontier

1963: transplanting kidneys

1964: the triumph of prevention – the case of strokes

1971: curing childhood cancer

1978: the first ‘Test-Tube’ baby

1984: Helicobacter – the cause of peptic ulcer

Wiki says: “in 1965, built upon the work of Hume and Popper, Hill suggested several aspects of causality in medicine and biology…” but his approach was not formal — he never referred to his principles as criteria — he recognized them as common sense behavior and his 1965 presentation to the Royal Society of Medicine, is a remarkably sober, intelligent document. Although described as an example of an article that, as here, has been read more often in quotations and paraphrases, it is worth reading the original even today.

Note: “Austin Bradford Hill’s surname was Hill and he always used the name Hill, AB in publications. However, he is often referred to as Bradford Hill. To add to the confusion, his friends called him Tony.” (This comment is from Wikipedia, not Woody Allen).

The President’s Address

Bradford Hill’s description of the factors that might make you think an association implied causality:

1. Strength. “First upon my list I would put the strength of the association.” This, of course, is exactly what is missing in the continued epidemiological scare stories. Hill describes

“….prospective inquiries into smoking have shown that the death rate from cancer of the lung in cigarette smokers is nine to ten times the rate in non-smokers and the rate in heavy cigarette smokers is twenty to thirty times as great.”

But further:

“On the other hand the death rate from coronary thrombosis in smokers is no more than twice, possibly less, the death rate in nonsmokers. Though there is good evidence to support causation it is surely much easier in this case to think of some features of life that may go hand-in-hand with smoking – features that might conceivably be the real underlying cause or, at the least, an important contributor, whether it be lack of exercise, nature of diet or other factors.”

Doubts about an odds ratio of two or less. That’s where you really have to wonder about causality. The progression of epidemiologic studies that tell you red meat, HFCS, etc. will cause diabetes, prostatic cancer, or whatever, these rarely hit an odds ratio of 2. While the published studies may contain disclaimers of the type in Hill’s paper, the PR department of the university where the work is done, and hence the public media, show no such hesitation and will quickly attribute causality to the study as if the odds ratio were 10 instead of 1.2.

2. Consistency: Hill listed the repetition of the results in other studies under different circumstances as a criterion for considering how much an association implied causality. Not mentioned but of great importance, is that this test cannot be made independent of the first criterion. Consistently weak associations do not generally add up to a strong association. If there is a single practice in modern medicine that is completely out of whack with respect to careful consideration of causality, it is the meta-analysis where studies with no strength at all are averaged so as to create a conclusion that is stronger than any of its components.

3. Specificity. Hill was circumspect on this point, recognizing that we should have an open mind on what causes what. On specificity of cancer and cigarettes, Hill noted that the two sites in which he showed a cause and effect relationship were the lungs and the nose.

4. Temporality: Obviously, we expect the cause to precede the effect or, as some wit put it “which got laid first, the chicken or the egg.” Hill recognized that it was not so clear for diseases that developed slowly. “Does a particular diet lead to disease or do the early stages of the disease lead to those peculiar dietetic habits?” Of current interest are the epidemiologic studies that show a correlation between diet soda and obesity which are quick to see a causal link but, naturally, one should ask “Who drinks diet soda?”

5. Biological gradient: the association should show a dose response curve. In the case of cigarettes, the death rate from cancer of the lung increases linearly with the number of cigarettes smoked. A subset of the first principle, that the association should be strong, is that the dose-response curve should have a meaningful slope and, I would add, the numbers should be big.

6. Plausibilityy: On the one hand, this seems critical — the association of egg consumption with diabetes is obviously foolish — but the hypothesis to be tested may have come from an intuition that is far from evident. Hill said, “What is biologically plausible depends upon the biological knowledge of the day.”

7. Coherence: “data should not seriously conflict with the generally known facts of the natural history and biology of the disease”

8. Experiment: It was another age. It is hard to believe that it was in my lifetime. “Occasionally it is possible to appeal to experimental, or semi-experimental, evidence. For example, because of an observed association some preventive action is taken. Does it in fact prevent?” The inventor of the random controlled trial would be amazed how many of these are done, how many fail to prevent. And, most of all, he would have been astounded that it doesn’t seem to matter. However, the progression of failures, from Framingham to the Women’s Health Initiative, the lack of association between low fat, low saturated fat and cardiovascular disease, is strong evidence for the absence of causation.

9. Analogy: “In some circumstances it would be fair to judge by analogy. With the effects of thalidomide and rubella before us we would surely be ready to accept slighter but similar evidence with another drug or another viral disease in pregnancy.”

Hill’s final word on what has come to be known as his criteria for deciding about causation:

“Here then are nine different viewpoints from all of which we should study association before we cry causation. What I do not believe — and this has been suggested — is that we can usefully lay down some hard-and-fast rules of evidence that must be obeyed before we accept cause and effect. None of my nine viewpoints can bring indisputable evidence for or against the cause-and-effect hypothesis and none can be required as a sine qua non. What they can do, with greater or less strength, is to help us to make up our minds on the fundamental question – is there any other way of explaining the set of facts before us, is there any other answer equally, or more, likely than cause and effect?” This may be the first critique of the still-to-be-invented Evidence-based Medicine.

Nutritional Epidemiology.

The decision to say that an observational study implies causation is equivalent to an assertion that the results are meaningful, that it is not a random association at all, that it is scientifically sound. Critics of epidemiological studies have relied on their own perceptions and appeal to common sense and when I started this blogpost, I was one of them, and I had not appreciated the importance of Bradford Hill’s principles. The Emperor of All Maladies described Hill’s strategies for dealing with association and causation “which have remained in use by epidemiologists to date.” But have they? The principles are in the texts. Epidemiology, Biostatistics, and Preventive Medicine has a chapter called “The study of causation in Epidemiologic Investigation and Research” from which the dose-response curve was modified. Are these principles being followed? Previous posts in this blog and others have have voiced criticisms of epidemiology as it’s currently practiced in nutrition but we were lacking a meaningful reference point. Looking back now, what we see is a large number of research groups doing epidemiology in violation of most of Hill’s criteria.

The red meat scare of 2011 was Pan, et al and I described in a previous post, the remarkable blog from Harvard . Their blog explained that the paper was unnecessarily scary because it had described things in terms of “relative risks, comparing death rates in the group eating the least meat with those eating the most. The absolute risks… sometimes help tell the story a bit more clearly. These numbers are somewhat less scary.” I felt it was appropriate to ask “Why does Dr. Pan not want to tell the story as clearly as possible? Isn’t that what you’re supposed to do in science? Why would you want to make it scary?” It was, of course, a rhetorical question.

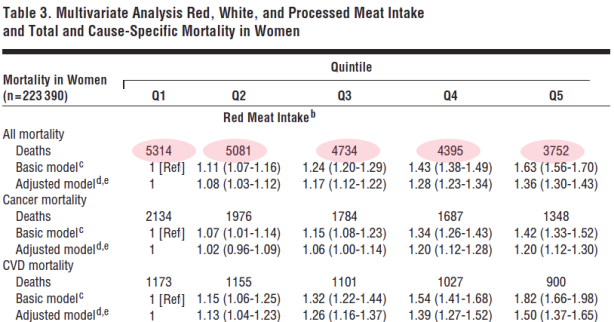
Looking at Pan, et al. in light of Bradford Hill, we can examine some of their data. Figure 2 from their paper shows the risk of diabetes as a function of red meat in the diet. The variable reported is the hazard ratio which can be considered roughly the same as the odds ratio, that is, relative odds of getting diabetes. I have indicated, in pink, those values that are not statistically significant and I grayed out the confidence interval to make it easy to see that these do not even hit the level of 2 that Bradford Hill saw as some kind of cut-off.

The hazard ratios for processed meat are somewhat higher but still less than 2. This is weak data and violates the first and most important of Hill’s criteria. As you go from quartile 2 to 3, there is an increase in risk, but at Q4, the risk goes down and then back up at Q5, in distinction to principle 5 which suggests the importance of dose-response curves. But, stepping back and asking what the whole idea is, asking why you would think that meat has a major — and isolatable role separate from everything else — in a disease of carbohydrate intolerance, you see that this is not rational, this is not science. And Pan is not making random observations. This is a test of the hypothesis that red meat causes diabetes. Most of us would say that it didn’t make any sense to test such a hypothesis but the results do not support the hypothesis.

What is science?

Science is a human activity and what we don’t like about philosophy of science is that it is about the structure and formalism of science rather than what scientists really do and so there aren’t even any real definitions. One description that I like, from a colleague at the NIH: “What you do in science, is you make a hypothesis and then you try to shoot yourself down.” One of the more interesting sidelights on the work of Hill and Doll, as described in Emperor, was that during breaks from the taxing work of analyzing the questionnaires that provided the background on smoking, Doll himself would step out for a smoke. Doll believed that cigarettes were unlikely to be a cause — he favored tar from paved highways as the causative agent — but as the data came in, “in the middle of the survey, sufficiently alarmed, he gave up smoking.” In science, you try to shoot yourself down and, in the end, you go with the data.

Uses and misuses of group statistics. Bill Gates walks into a bar…

Posted: January 28, 2013 in Fructose, misuse of statistics
Tags: carbohydrate, fructose, nutritional studies, statistics

Everybody has their favorite example of how averages don’t really tell you what you want to know or how they are inappropriate for some situations. Most of these are funny because they apply averages to cases where single events are important. I’ll list a couple in the text boxes in this post. From the title:

If Bill Gates walks into a bar, on average, everybody in the bar is a millionaire.

Technically speaking, averages start with the assumption that deviations are due to random error, that is, that there is a kind of “true” value if we could only control things well — if there were no wind resistance and all balls were absolutely uniform, they would always fall in the same place; any spread in values is random rather than systematic.

(more…)

Flawed studies II. Occam’s Razor and How to Reduce Fructose Consumption.

Posted: July 27, 2012 in Crisis in Nutrition, Fructose, lipid metabolism, low-carbohydrate diet, Lustig, Occam's Razor, Reduce Fructose Consumption
Tags: carbohydrate, low carbohydrate, nutritional studies, statistics

“I may have killed a dozen men but I never stole a horse.”

— last words of outlaw in the American West before being hanged.

The principle known as Occam’s Razor is usually understood as a statement that a simple explanation is preferable to one that is more complicated. The principle has many variations. It might be interpreted as saying that you have to have a sense of priorities. Occam’s Razor is not exactly a scientific idea so much as a principle of aesthetics expressing the value of elegance in scientific explanations. Named for William of Ockham (c. 1285–1349) — it is also referred to as Ockham’s Razor — the idea can be described mathematically by saying that if the outcome, Y, of an experiment can be expressed with a rough sort of equation: Y = A + B + C +… and if A explains Y, then you don’t want to drag in B, C, etc unless you absolutely have to. (A more compelling description might be to consider the principle in terms of a power series and if you are inclined to mathematics, Wikipedia has excellent description and animation).

Where we’re going. The bottom line on this post is that for obesity, diabetes and general health, the predominant effect of diet, the major contribution to the outcome — A in the equation above — is provided by substituting fat (any fat) for carbohydrate (any carbohydrate). That’s what the science says. That will give you the best effect. The B contribution (type of fat, type of carbohydrate) is strictly secondary. The practical consequence: if for some reason, you want to reduce fructose in the diet, the best advice is to reduce carbohydrate across the board. You can then add the additional advice “preferably sugar and high fructose corn syrup” but even if B doesn’t kick in, you will surely get a benefit. Most of all, if you take out Pepsi® and put in Pepperidge Farm® Whole Wheat Bread, you may not accomplish much.

In practical terms, confronted with a phenomenon that has many controlling variables, make sure you can’t do with one before you bring in the others. In nutrition, when people say that the phenomenon is very complicated, they frequently mean that they don’t want to look at a simple explanation. On its practical side, if a patients in a dietary experiment responds to the level of carbohydrate, you have to assume that carbohydrate across the board is the controlling variable. If, however, you think that it is specifically the fructose in the diet that caused the effect, or if you think that it was an additional effect of fructose beyond its role as carbohydrate, then that is something that you have to show separately. Until you do, the fructose effect is sliced off by Occam’s Razor. In terms of policy, you don’t want to go after fructose unless you are sure that it is not primarily the role of fructose acting as a carbohydrate.

So, there is a logical question surrounding recommendations against sugar and especially against fructose. What we know well in nutrition is that if you replace carbohydrate with fat, as in Krauss’s experiment described in the previous post, things improve and this is why we suggest low-carbohydrate diets as the “default diet,” the one to try first for diabetes and metabolic syndrome and probably for cardiovascular risk. I have, however, received at least two emails from well-known nutritionists saying that “the type of carbohydrate is more important than how much carbohydrate” and, of course, Rob Lustig is everywhere telling us how toxic sugar is but never suggesting that a low carbohydrate diet is any kind of ideal. On the face of it, the idea doesn’t make much sense. Fructose is a carbohydrate so the amount and type are not easily separable.

There are all kinds of strange things in nutrition. People actually say that the type of diet you are on is less important than whether you stay on the diet. While true, it is like saying that if you are baseball player, whether you get a hit depends less on who’s pitching than whether you remember to show up for the game. But anyway, I decided to ask the question about relative importance of type and amount of carbohydrate on facebook and on a couple of blogs where things like Hizzona’ Michael Bloomberg’s Big Bottle Ban or related questions was being discussed. Here’s how I put it.

For general health, should you change the type of carbohydrate or replace the carbohydrate with fat (any natural fat, no trans-fat)? It’s a thought experiment (not real world situation with subtleties). You only get three choices: For general health (no change in calories):

1. Change type of carbohydrate
2. Replace carbohydrate with fat
3. It doesn’t matter

Strangely enough, I did not get very many answers. I think that people didn’t like the question and even when they voted, they wanted to put in disclaimers:

ANS: 2. Replace carbohydrate with fat But I want to add; not replacing ALL the carbs. Only the worst ones. You know; Sugar, grains (bread and pasta) potatoes and rice.

RDF: You can do that in a real case but the question is about first-order strategies. You only get 3 choices.

ANS: okej 2. Replace carbohydrate with fat.

And James Krieger jumped in:

“Feinman, your ‘thought experiment’ is essentially a false trichotomy…same thing as a false dichotomy except you’ve arbitrarily limited it to 3 choices rather than 2, when in fact there are many more. This is why you aren’t getting answers…because you’re committing a common logical fallacy.”

I explained that

“It’s called Occam’s Razor…. I’m simply asking: if you could theoretically do only one thing, 1. or 2., which would be better? There are many other choices but in a thought experiment you imagine these to be held constant or to be the higher order terms in a power series.”

But, of course, Krieger was right. The question is not really answerable. Not because it is false so much as because it is confused. Fructose is a carbohydrate and whatever its unique contribution, it is hard to say it is more important than the contribution of the fructose as a carbohydrate. It is a screwy idea but, again, that’s how it was phrased to me in emails and probably in print someplace. Researchers in this field say: “it is not carbohydrate per se (or glycemic index/load) that is involved in adverse metabolic effects of dietary carbohydrates, but rather the type of carbohydrate,…” The kind of evidence that is used to support such an idea, the kind of result that is used to support fructophobia is in the paper by Stanhope, et al.

Stanhope, et al. measured the effects of chronic consumption of either glucose- or fructose-sweetened beverages providing 25% of energy requirements for 10 weeks in overweight and obese subjects. The figure below shows the superimposed outcomes in the response of triglycerides in the course of a day (red lines = fructose, blue = glucose). It is obvious that there is a difference — people consuming fructose had higher triglyceride responses (although fasting levels were not different). Looking at the figure, though, there is big variation in the data and it is not clear that everybody showed big differences between the glucose and fructose curves: the error bars represent standard error of the mean (SEM) which, while it shows you that there may be a statistically significant difference between the trials, doesn’t display very well the spread of the individual values, that is, whether a few individuals biased the grouped data. To convert to standard deviation, which gives you a better feel for the variation, you multiply, in this case, by about 4. In other words, there must have been big overlap between the fructose people and the glucose people.

So there is an effect of type of carbohydrate. But what to compare it to? The study of Krauss in the previous post showed much bigger changes when you substituted fat for carbohydrate and, in fact, those were fasting triglycerides which, in the fructose experiment, didn’t change at all but this is a different kind of experiment. So for comparison, we can look at a study from Jeff Volek’s lab where carbohydrate was replaced with fat in the carbohydrate restricted diet (CRD) in comparison to a low-fat diet (LFD). I described this study previously because it showed how carbohydrate, rather than dietary saturated fat, was actually controlling saturated fat in the blood. Here is what the responses to meals as seen in plasma triglycerides:

Maybe it’s the Fructose.

The fructose experiments can be shaved with Occam’s razor — insofar as we can tell, reducing carbohydrate across the board is more effective than changing type of carbohydrate. But how do we know that the effect of reducing carbohydrates wasn’t due to removing fructose — fructose is a carbohydrate so carbohydrate restriction may be due to the de facto removal of the fructose? Well, we don’t. It’s unlikely but possible. Where does this leave us? Wikipedia cites Bertrand Russell’s variation of Occam’s Razor: “Whenever possible, substitute constructions out of known entities for inferences to unknown entities.” This is a pompous way of saying: “don’t make things up.”

Another way of looking at Stanhope’s experiment is to recognize that it does not show, as the title says, “Consuming fructose-sweetened, not glucose-sweetened, beverages increases visceral adiposity and lipids… in overweight/obese humans.” What the paper really is about is “Consuming fructose-sweetened, not glucose-sweetened, beverages as part a high carbohydrate diet (55 % of energy) increases….” In other words, you don’t know whether you would get any benefit in changing from fructose to glucose if the total carbohydrate were lower. In terms of our Occam’s Razor equation, you can’t say that you have proved that your results are due to A (the major controlling variable (carbohydrate)) when all you have studied is A with the specific change in the B term (secondary effect of the type of carbohydrate). Stanhope’s experiment shows: if you are on a high carbohydrate diet, replacing glucose with fructose will make things worse but that’s different than saying that fructose is toxic. From a practical point of view, if you are on a high carbohydrate diet and it is not giving you the health benefit you want, replacing sugar with starch may give you disappointing results compared to simply cutting down on carbohydrates.

How to Reduce Fructose Consumption.

If you want to encourage fructose reduction, encourage carbohydrate restriction (this is where we have the most information) with the additional proviso of recommending fructose reduction as the first carbohydrate to remove (may also help but we have less data).

Flawed Studies.

In combination with the previous post, a summary of things to look for in a study to make sure that the authors are not misleading you and/or themselves:

1. Understatement is good. “Healthy” is a value judgement. “Fructose-sweetened” is not the same thing as “fructose-sweetened in a high carbohydrate diet.”

2. Where are the pictures? The author has an obligation to make things clear. A graphic representation is usually an indication of a desire to explain.

3. Has Occam’s Razor been applied? Are secondary effects taken as primary?

Crabtree’s Bludgeon

Finally, we should not forget Crabtree’s Bludgeon which is described by Wikipedia as “a foil to Occam’s Razor” and “attributed to the fictitious poet, Joseph Crabtree, after whom the Crabtree Foundation is named.” It may be expressed as:

‘No set of mutually inconsistent observations can exist for which some human intellect cannot conceive a coherent explanation, however complicated.’

Reading the Scientific Literature. A Guide to Flawed Studies.

Posted: July 11, 2012 in Association and Causality, The Nutrition Story, triglycerides
Tags: low carbohydrate, nutrition, scientific literature, statistics

Doctor: Therein the patient

Must minister to himself.

Macbeth: Throw physic [medicine] to the dogs; I’ll none of it.

— William Shakespeare, Macbeth

The quality of nutrition papers even in the major scientific and medical journals is so variable and the lack of restraint in the popular media is so great that it is hard to see how the general public or even scientists can find out anything at all. Editors and reviewers are the traditional gate-keepers in science but in an area where rigid dogma has reached Galilean proportions, it is questionable that any meaningful judgement was made: it is easy to publish papers that conform to the party line (“Because of the deleterious effects of dietary fructose, we hypothesized that…”) and hard to publish others: when JAMA published George Bray’s “calorie-is-a-calorie” paper and I pointed out that the study more accurately supported the importance of carbohydrate as a controlling variable, the editor declined to publish my letter. In this, the blogs have performed a valuable service in providing an alternative POV but if the unreliability is a problem in the scientific literature, that problem is multiplied in internet sources. In the end, the consumer may feel that they are pretty much out there on their own. I will try to help. The following was posted on FatHead’s Facebook page:

How does one know if a study is ‘flawed’? I see a lot of posts on here that say a lot of major studies are flawed. How? Why? What’s the difference if I am gullible and believe all the flawed studies, or if I (am hopefully not a sucker) believe what the Fat Heads are saying and not to believe the flawed studies — eat bacon.

Where are the true studies that are NOT flawed…. and how do I differentiate? : /

My comment was that it was a great question and that it would be in the next post so I will try to give some of the principles that reviewers should adhere to. Here’s a couple of guides to get started. More in future posts:

1. “Healthy” (or “healthful”) is not a scientific term. If a study describes a diet as “healthy,” it is almost guaranteed to be a flawed study. If we knew which diets were “healthy,” we wouldn’t have an obesity epidemic. A good example is the paper by Appel, et al. (2005). “Effects of protein, monounsaturated fat, and carbohydrate intake on blood pressure and serum lipids: results of the OmniHeart randomized trial,” whose conclusion is:

“In the setting of a healthful diet, partial substitution of carbohydrate with either protein or monounsaturated fat can further lower blood pressure, improve lipid levels, and reduce estimated cardiovascular risk.”

It’s hard to know how healthful the original diet, a “carbohydrate-rich diet used in the DASH trials … currently advocated in several scientific reports” really is if removing carbohydrate improved everything.

Generally, understatement is good. One of the more famous is from Watson & Cricks’s 1953 paper in which they proposed the DNA double helix structure. They said “It has not escaped our notice that the specific pairing we have postulated immediately suggests a possible copying mechanism for the genetic material.” A study with the word “healthy” is an infomercial.

2. Look for the pictures (figures). Presentation in graphic form usually means the author wants to explain things to you, rather than snow you. This is part of the Golden Rule of Statistics that I mentioned in my blogpost “The Seventh Egg” which discusses a very flawed study from Harvard on egg consumption. The rule comes from the book PDQ Statistics:

“The important point…is that the onus is on the author to convey to the reader an accurate impression of what the data look like, using graphs or standard measures, before beginning the statistical shenanigans. Any paper that doesn’t do this should be viewed from the outset with considerable suspicion.”

The Watson-Crick paper cited above had the diagram of the double-helix which essentially became the symbol of modern biology. It was drawn by Odile, Francis’s wife, who is described as being famous for her nudes, only one of which I could find on the internet.

Krauss, et. al. Separate effects of reduced carbohydrate intake and weight loss on atherogenic dyslipidemia.

The absence of a figure may indicate that the authors are not giving you a chance to actually see the results, that is, the experiment may not be flawed but the interpretation may be misleading, intentionally or otherwise. An important illustration of the principle is a paper published by Krauss. It is worth looking at this paper in detail because the experimental work is very good and the paper directly — or almost directly — confronts a big question in diet studies: when you reduce calories by cutting out carbohydrate, is the effect due simply to lowering calories or is there a specific effect of carbohydrate restriction. The problem is important since many studies compare low-carbohydrate and low-fat diets where calories are reduced on both. Because the low-carbohydrate diet generally has the better weight loss and better improvement in HDL and triglycerides, it is said that it was the weight loss that caused the lipid improvements.

So Krauss compared the effects of carbohydrate restriction and weight loss on the collection of lipid markers known collectively as atherogenic dyslipidemia. The markers of atherogenic dyslipidemia, which are assumed to predispose to cardiovascular disease, include high triglycerides (triacylglycerol), low HDL and high concentrations of the small dense LDL.

Here is how the experiment was set up: subjects first consumed a baseline diet of 54% of energy as carbohydrate, for 1 week. They were then assigned to one of four groups. Either they continued the baseline diet, or they kept calories constant but reduced carbohydrate by putting fat in its place. The three lower carbohydrate diets had 39 % or 26 % carbohydrate or 26 % carbohydrate with higher saturated fat. After 3 weeks on constant calories but reduced carbohydrate, calories were decreased by 1000 kcal/d for 5 week and, finally, energy was stabilized for 4 weeks and the features of atherogenic dyslidemia were measured at week 13. The protocol is shown in the figure from Krauss’s paper:

The Abstract of the paper describes the outcomes and the authors’ conclusions.

Results: The 26%-carbohydrate, low-saturated-fat diet reduced [atherogenic dylipidemia]. These changes were significantly different from those with the 54%-carbohydrate diet. After subsequent weight loss, the changes in all these variables were significantly greater…(my italics)

Conclusions: Moderate carbohydrate restriction and weight loss provide equivalent but non-additive approaches to improving atherogenic dyslipidemia. Moreover, beneficial lipid changes resulting from a reduced carbohydrate intake were not significant after weight loss.

Now there is something odd about this. It is the last line of the conclusion that is really weird. If you lose weight, the effect of carbohydrate is not significant? As described below, Jeff Volek and I re-analyzed this paper so I have read that line a dozen times and I have no idea what it means. In fact, the whole abstract is strange. It will turn out that the lower (26 %) is certainly “significantly different from.. the 54%-carbohydrate diet” but it is not just different but much better. Why would you not say that? The Abstract is generally written so that it sounds negative about low carbohydrate effects but it is already known from Krauss’s previous work and others that carbohydrate restriction has a beneficial effect on lipids and the improvements in lipid markers occur on low-carbohydrate diets whether weight is lost or not. The last sentence doesn’t seem to make any sense at all. For one thing, the experiment wasn’t done that way. As set up, weight loss came after carbohydrate restriction. So, let’s look at the data in the paper. There are few figures in the paper and Table 2 in the paper presents the results in a totally mind-numbing layout. Confronted with data like this, I sometimes stop reading. After all, if the author doesn’t want to conform to the Golden Rule of Statistics, if they don’t want to really explain what they accomplished, how much impact is the paper going to have. In this case, however, it is clear that the experiment was designed correctly and it just seems impossible from previous work that this wouldn’t support the benefits of carbohydrate restriction and the negative tone of the Abstract needs to be explained. So we all had to slog through those tables. Let’s just look at the triglycerides since this is one of the more telling attributes of atherogenic dyslpidemia. Here’s the section from the Table:

Well this looks odd in that the biggest change is in the lowest carb group with high SF but it’s hard to tell what the data look like. First it is reported as logarithms. You sometime take logs of your data in order to do a statistical determination but that doesn’t change the data and it is better to report the actual value. In any case, it’s easy enough to take antilogs and we can plot the data. This is what it looks like:

It’s not hard to see what the data really show: Reducing carbohydrate has an overwhelming effect on triglycerides even without weight loss. When weight loss is introduced, the high carbohydrate diets still can’t equal the performance of the carbohydrate reduction phase. (The dotted line in the figure are data from Volek’s earlier work which Krauss forgot to cite).

The statements in the Conclusion from the Abstract are false and totally misrepresent the data. It is not true as it says “carbohydrate restriction and weight loss provide equivalent…” effects. The carbohydrate-reduction phase is dramatically better than the calorie restriction phase and it is not true that they are “non-additive” Is this an oversight? Poor writing? Well, nobody knows what Krauss’s motivations were but Volek and I plotted all of the data from Krauss’s paper and we published a paper in Nutrition & Metabolism providing an interpretation of Krauss’s work (with pictures). Our conclusion:

Summary Although some effort is required to disentangle the data and interpretation, the recent publication from Krauss et al. should be recognized as a breakthrough. Their findings… make it clear that the salutary effects of CR on dyslipidemia do not require weight loss, a benefit that is not a feature of strategies based on fat reduction. As such, Krauss et al. provides one of the strongest arguments to date for CR as a fundamental approach to diet, especially for treating atherogenic dyslipidemia.

An important question in this experiment, however, is whether even in the calorie reduction phase, calories are actually the important variable. This is a general problem in calorie restriction studies if for no other reason than that there is no identified calorie receptor. When we published this data, Mike Eades pointed out that in the phase in which Krauss reduced calories, it was done by reducing macronutrients across the board so carbohydrate was also reduced and that might be the actual controlling variable so we plotted the TAG against carbohydrate in each phase (low, medium and high carb (LC, MC, HC) without or with weight loss (+WL) and the results are shown below

This is remarkably good agreement for a nutrition study. When you consider carbohydrates as the independent variable, you can see what’s going on. Or can you? After all, by changing the variables you have only made an association between carbohydrate and outcome of an experiment. So does this imply a causal relation between carbohydrate and triglycerides or not? It is widely said that observational studies do not imply causality, that observational studies can only provide hypothesis for future testing. It certainly seems like causality is implied here. It will turn out that a more accurate description is that observational studies do not necessarily imply causality and I will discuss that in the next posts. The bottom line will be that there is flaw in grand principles like “Random controlled trials are the gold standard.” “Observational studies are only good for generating hypotheses,” “Metabolic Ward Studies are the gold standard.” Science doesn’t run on such arbitrary rules.

Making Americans Afraid of Meat.

Posted: May 13, 2012 in Association and Causality, Crisis in Nutrition, Red Meat, saturated fat
Tags: carbohydrate, Meat Intake and Mortality, red meat,, statistics

TIME: You’re partnering with, among others, Harvard University on this. In an alternate Lady Gaga universe, would you have liked to have gone to Harvard?

Lady Gaga: I don’t know. I am going to Harvard today. So that’ll do.

— Belinda Luscombe, Time Magazine, March 12, 2012

There was a sense of déja-vu about the latest red meat scare and I thought that my previous post as well as those of others had covered the bases but I just came across a remarkable article from the Harvard Health Blog. It was entitled “Study urges moderation in red meat intake.” It describes how the “study linking red meat and mortality lit up the media…. Headline writers had a field day, with entries like ‘Red meat death study,’ ‘Will red meat kill you?’ and ‘Singing the blues about red meat.”’

What’s odd is that this is all described from a distance as if the study by Pan, et al (and likely the content of the blog) hadn’t come from Harvard itself but was rather a natural phenomenon, similar to the way every seminar on obesity begins with a slide of the state-by-state development of obesity as if it were some kind of meteorologic event.

When the article refers to “headline writers,” we are probably supposed to imagine sleazy tabloid publishers like the ones who are always pushing the limits of first amendment rights in the old Law & Order episodes. The Newsletter article, however, is not any less exaggerated itself. (My friends in English Departments tell me that self-reference is some kind of hallmark of real art). And it is not true that the Harvard study was urging moderation. In fact, it is admitted that the original paper “sounded ominous. Every extra daily serving of unprocessed red meat (steak, hamburger, pork, etc.) increased the risk of dying prematurely by 13%. Processed red meat (hot dogs, sausage, bacon, and the like) upped the risk by 20%.” That is what the paper urged. Not moderation. Prohibition. Who wants to buck odds like that? Who wants to die prematurely?

It wasn’t just the media. Critics in the blogosphere were also working over-time deconstructing the study. Among the faults that were cited, a fault common to much of the medical literature and the popular press, was the reporting of relative risk.

The limitations of reporting relative risk or odds ratio are widely discussed in popular and technical statistical books and I ran through the analysis in the earlier post. Relative risk destroys information. It obscures what the risks were to begin with. I usually point out that you can double your odds of winning the lottery if you buy two tickets instead of one. So why do people keep doing it? One reason, of course, is that it makes your work look more significant. But, if you don’t report the absolute change in risk, you may be scaring people about risks that aren’t real. The nutritional establishment is not good at facing their critics but on this one, they admit that they don’t wish to contest the issue.

Nolo Contendere.

“To err is human, said the duck as it got off the chicken’s back”

— Curt Jürgens in The Devil’s General

Having turned the media loose to scare the American public, Harvard now admits that the bloggers are correct. The Health NewsBlog allocutes to having reported “relative risks, comparing death rates in the group eating the least meat with those eating the most. The absolute risks… sometimes help tell the story a bit more clearly. These numbers are somewhat less scary.” Why does Dr. Pan not want to tell the story as clearly as possible? Isn’t that what you’re supposed to do in science? Why would you want to make it scary?

The figure from the Health News Blog:

	Deaths per 1,000 people per year
	1 serving unprocessed meat a week	2 servings unprocessed meat a day
Women	7.0	8.5
	3 servings unprocessed meat a week	2 servings unprocessed meat a day
Men	12.3	13.0

Unfortunately, the Health Blog doesn’t actually calculate the absolute risk for you. You would think that they would want to make up for Dr. Pan scaring you. Let’s calculate the absolute risk. It’s not hard.Risk is usually taken as probability, that is, number cases divided by total number of participants. Looking at the men, the risk of death with 3 servings per week is equal to the 12.3 cases per 1000 people = 12.3/1000 = 0.1.23 = 1.23 %. Now going to 14 servings a week (the units in the two columns of the table are different) is 13/1000 = 1.3 % so, for men, the absolute difference in risk is 1.3-1.23 = 0.07, less than 0.1 %. Definitely less scary. In fact, not scary at all. Put another way, you would have to drastically change the eating habits (from 14 to 3 servings) of 1, 429 men to save one life. Well, it’s something. Right? After all for millions of people, it could add up. Or could it? We have to step back and ask what is predictable about 1 % risk. Doesn’t it mean that if a couple of guys got hit by cars in one or another of the groups whether that might not throw the whole thing off? in other words, it means nothing.

Observational Studies Test Hypotheses but the Hypotheses Must be Testable.

It is commonly said that observational studies only generate hypotheses and that association does not imply causation. Whatever the philosophical idea behind these statements, it is not exactly what is done in science. There are an infinite number of observations you can make. When you compare two phenomena, you usually have an idea in mind (however much it is unstated). As Einstein put it “your theory determines the measurement you make.” Pan, et al. were testing the hypothesis that red meat increases mortality. If they had done the right analysis, they would have admitted that the test had failed and the hypothesis was not true. The association was very weak and the underlying mechanism was, in fact, not borne out. In some sense, in science, there is only association. God does not whisper in our ear that the electron is charged. We make an association between an electron source and the response of a detector. Association does not necessarily imply causality, however; the association has to be strong and the underlying mechanism that made us make the association in the first place, must make sense.

What is the mechanism that would make you think that red meat increased mortality. One of the most remarkable statements in the original paper:

“Regarding CVD mortality, we previously reported that red meat intake was associated with an increased risk of coronary heart disease^{2, 14} and saturated fat and cholesterol from red meat may partially explain this association. The association between red meat and CVD mortality was moderately attenuated after further adjustment for saturated fat and cholesterol, suggesting a mediating role for these nutrients.” (my italics)

This bizarre statement — that saturated fat played a role in increased risk because it reduced risk— was morphed in the Harvard News Letters plea bargain to “The authors of the Archives paper suggest that the increased risk from red meat may come from the saturated fat, cholesterol, and iron it delivers;” the blogger forgot to add “…although the data show the opposite.” Reference (2) cited above had the conclusion that “Consumption of processed meats, but not red meats, is associated with higher incidence of CHD and diabetes mellitus.” In essence, the hypothesis is not falsifiable — any association at all will be accepted as proof. The conclusion may be accepted if you do not look at the data.

The Data

In fact, the data are not available. The individual points for each people’s red meat intake are grouped together in quintiles ( broken up into five groups) so that it is not clear what the individual variation is and therefore what your real expectation of actually living longer with less meat is. Quintiles are some kind of anachronism presumably from a period when computers were expensive and it was hard to print out all the data (or, sometimes, a representative sample). If the data were really shown, it would be possible to recognize that it had a shotgun quality, that the results were all over the place and that whatever the statistical correlation, it is unlikely to be meaningful in any real world sense. But you can’t even see the quintiles, at least not the raw data. The outcome is corrected for all kinds of things, smoking, age, etc. This might actually be a conservative approach — the raw data might show more risk — but only the computer knows for sure.

Confounders

“…mathematically, though, there is no distinction between confounding and explanatory variables.”

— Walter Willett, Nutritional Epidemiology, 2^o edition.

You make a lot of assumptions when you carry out a “multivariate adjustment for major lifestyle and dietary risk factors.” Right off , you assume that the parameter that you want to look at — in this case, red meat — is the one that everybody wants to look at, and that other factors can be subtracted out. However, the process of adjustment is symmetrical: a study of the risk of red meat corrected for smoking might alternatively be described as a study of the risk from smoking corrected for the effect of red meat. Given that smoking is an established risk factor, it is unlikely that the odds ratio for meat is even in the same ballpark as what would be found for smoking. The figure below shows how risk factors follow the quintiles of meat consumption. If the quintiles had been derived from the factors themselves we would have expected even better association with mortality.

The key assumption is that the there are many independent risk factors which contribute in a linear way but, in fact, if they interact, the assumption is not appropriate. You can correct for “current smoker,” but biologically speaking, you cannot correct for the effect of smoking on an increased response to otherwise harmless elements in meat, if there actually were any. And, as pointed out before, red meat on a sandwich may be different from red meat on a bed of cauliflower puree.

This is the essence of it. The underlying philosophy of this type of analysis is “you are what you eat.” The major challenge to this idea is that carbohydrates, in particular, control the response to other nutrients but, in the face of the plea of nolo contendere, it is all moot.

Who paid for this and what should be done.

We paid for it. Pan, et al was funded in part by 6 NIH grants. (No wonder there is no money for studies of carbohydrate restriction). It is hard to believe with all the flaws pointed out here and, in the end, admitted by the Harvard Health Blog and others, that this was subject to any meaningful peer review. A plea of no contest does not imply negligence or intent to do harm but something is wrong. The clear attempt to influence the dietary habits of the population is not justified by an absolute risk reduction of less than one-tenth of one per cent, especially given that others have made the case that some part of the population, particularly the elderly may not get adequate protein. The need for an oversight committee of impartial scientists is the most important conclusion of Pan, et al. I will suggest it to the NIH.

Intention-to-treat II: Foster, et al: Weight and Metabolic Outcomes After 2 Years

Posted: August 28, 2011 in Evidence Based Medicine, Intention to Treat, low-carbohydrate diet, The Nutrition Story
Tags: carbohydrate, dietary guidelines, In the face of contradictory evidence, JAMA, low-fat, nutrition, statistics

“Doctors prefer large studies that are bad to small studies that are good.”

— anon.

The paper by Foster and coworkers entitled Weight and Metabolic Outcomes After 2 Years on a Low-Carbohydrate Versus Low-Fat Diet, published in 2010, had a surprisingly limited impact, especially given the effect of their first paper in 2003 on a one-year study. I have described the first low carbohydrate revolution as taking place around that time and, if Gary Taubes’s article in the New York Times Magazine was the analog of Thomas Paine’s Common Sense, Foster’s 2003 paper was the shot hear ’round the world.

The paper showed that the widely accepted idea that the Atkins diet, admittedly good for weight loss, was a risk for cardiovascular disease, was not true. The 2003 Abstract said “The low-carbohydrate diet was associated with a greater improvement in some risk factors for coronary heart disease.” The publication generated an explosive popularity of the Atkins diet, ironic in that Foster had said publicly that he undertook the study in order to “once and for all,” get rid of the Atkins diet. The 2010 paper by extending the study to 2 years would seem to be very newsworthy. So what was wrong? Why is the new paper more or less forgotten? Two things. First, the paper was highly biased and its methods were so obviously flawed — obvious even to the popular press — that it may have been a bit much even for the media. It remains to be seen whether it will really be cited but I will suggest here that it is a classic in misleading research and in the foolishness of intention-to-treat (ITT).

(more…)

Nothing wrong with Observational Studies. And Association does Imply Causality but…

Posted: June 19, 2011 in Association and Causality, Evidence Based Medicine, Intention to Treat, low-carbohydrate diet, Observational Studies, thermodynamics
Tags: low carbohydrate, red meat,, statistics

…the association has to be strong and the causality has to be plausible and consistent. And you have to have some reason to make the observation; you can’t look at everything. And experimentally, observation may be all that you have — almost all of astronomy is observational. Of course, the great deconstructions of crazy nutritional science — several from Mike Eades blog and Tom Naughton’s hysterically funny-but-true course in how to be a scientist — are still right on but, strictly speaking, it is the faulty logic of the studies and the whacko observations that is the problem, not simply that they are observational. It is the strength and reliability of the association that tells you whether causality is implied. Reducing carbohydrates lowers triglycerides. There is a causal link. You have to be capable of the state of mind of the low-fat politburo not to see this (for example, Circulation, May 24, 2011; 123(20): 2292 – 2333).

It is frequently said that observational studies are only good for generating hypotheses but it is really the other way around. All studies are generated by hypotheses. As Einstein put it: your theory determines what you measure. I ran my post on the red meat story passed April Smith and her reaction was “why red meat? Why not pancakes” which is exactly right. Any number of things can be observed. Once you pick, you have a hypothesis.

Where did the first law of thermodynamics come from?

Thermodynamics is an interesting case. The history of the second law involves a complicated interplay of observation and theory. The idea that there was an absolute limit to how efficient you could make a machine and by extension that all real processes were necessarily inefficient largely comes from the brain power of Carnot. He saw that you could not extract as work all of the heat you put into a machine. Clausius encapsulated it into the idea of the entropy as in my Youtube video.

The origins of the first law, the conservation of energy, are a little stranger. It turns out that it was described more than twenty years after the second law and it has been attributed to several people, for a while, to the German physicist von Helmholtz. These days, credit is given to a somewhat eccentric German physician named Robert Julius Mayer. Although trained as a doctor, Mayer did not like to deal with patients and was instead more interested in physics and religion which he seemed to think were the same thing. He took a job as a shipboard physician on an expedition to the South Seas since that would give him time to work on his main interests. It was in Jakarta where, while treating an epidemic with the practice then of blood letting, that he noticed that the venous blood of the sailors was much brighter than when they were in colder climates as if “I had struck an artery.” He attributed this to a reduced need for the sailors to use oxygen for heat and from this observation, he somehow leapt to the grand principle of conservation of energy, that the total amount of heat and work and any other forms of energy does not change but can only be interconverted. It is still unknown what kind of connections in his brain led him to this conclusion. The period (1848) corresponds to the point at which science separated from philosophy. Mayer seems to have had one foot in each world and described things in the following incomprehensible way:

If two bodies find themselves in a given difference, then they could remain in a state of rest after the annihilation of [that] difference if the forces that were communicated to them as a result of the leveling of the difference could cease to exist; but if they are assumed to be indestructible, then the still persisting forces, as causes of changes in relationship, will again reestablish the original present difference.

(I have not looked for it but one can only imagine what the original German was like). Warmth Disperses and Time Passes. The History of Heat, Von Baeyer’s popular book on thermodynamics, describes the ups and downs of Mayer’s life, including the death of three of his children which, in combination with rejection of his ideas, led to hospitalization but ultimate recognition and knighthood. Surely this was a great observational study although, as von Baeyer put it, it did require “the jumbled flashes of insight in that sweltering ship’s cabin on the other side of the world.”

It is also true that association does imply causation but, again, the association has to have some impact and the proposed causality has to make sense. In some way, purely observational experiments are rare. As Pasteur pointed out, even serendipity is favored by preparation. Most observational experiments must be a reflection of some hypothesis. Otherwise you’re wasting tax-payer’s money; a kiss of death on a grant application is to imply that “it would be good to look at.…” You always have to have something in mind. The great observational studies like the Framingham Study are bad because they have no null hypothesis. When the Framingham study first showed that there was no association between dietary total and saturated fat or dietary cholesterol, the hypothesis was quickly defended. The investigators were so tied to a preconceived hypothesis, that there was hardly any point in making the observations.

In fact, a negative result is always stronger than one showing consistency; consistent sunrises will go by the wayside if the sun fails to come up once. It is the lack of an association between the decrease in fat consumption during the epidemic of obesity and diabetes that is so striking. The figure above shows that the increase in carbohydrate consumption is consistent with the causal role of dietary carbohydrate in creating anabolic hormonal effects and with the poor satiating effects of carbohydrates — almost all of the increase of calories during the epidemic of obesity and diabetes has been due to carbohydrates. However, this observation is not as strong as the lack of an identifiable association of obesity and diabetes with fat consumption. It is the 14 % decrease in the absolute amount of saturated fat for men that is the problem. If the decrease in fat were associated with decrease in obesity, diabetes and cardiovascular disease, there is little doubt that the USDA would be quick to identify causality. In fact, whereas you can find the occasional low-fat trial that succeeds, if the diet-heart hypothesis were as described, they should not fail. There should not be a single Women’s Health Initiative, there should not be a single Framingham study, not one.

Sometimes more association would be better. Take intention-to-treat. Please. In this strange statistical idea, if you assign a person to a particular intervention, diet or drug, then you must include the outcome data (weight loss, change in blood pressure) for that person even if the do not comply with the protocol (go off the diet, stop taking the pills). Why would anybody propose such a thing, never mind actually insist on it as some medical journals or granting agencies do? When you actually ask people who support ITT, you don’t get coherent answers. They say that if you just look at per protocol data (only from people who stayed in the experiment), then by excluding the drop-outs, you would introduce bias but when you ask them to explain that you get something along the lines of Darwin and the peas growing on the wrong side of the pod. The basic idea, if there is one, is that the reason that people gave up on their diet or stopped taking the pills was because of an inherent feature of the intervention: made them sick, drowsy or something like that. While this is one possible hypothesis and should be tested, there are millions of others — the doctor was subtly discouraging about the diet, or the participants were like some of my relatives who can’t remember where they put their pills, or the diet book was written in Russian, or the diet book was not written in Russian etc. I will discuss ITT in a future post but for the issue at hand: if you do a per-protocol you will observe what happens to people when stay on their diet and you will have an association between the content of the diet and performance. With an ITT analysis, you will be able to observe what happens when people are told to follow a diet and you will have an association between assignment to a diet and performance. Both are observational experiments with an association between variables but they have different likelihood of providing a sense of causality.

Evidence Based Medicine and Admissibility. IV. The Oslo Diet-Heart Study.

Posted: June 1, 2011 in Evidence Based Medicine, Lipophobes, The Nutrition Story
Tags: cholesterol, diet-heart, nutritional studies, Oslo, statistics, Steinberg

“In the Viking era, they were already using skis…and over the centuries, the Norwegians have proved themselves good at little else.”

–John Cleese, Norway, Home of Giants.

With the 3-foot bookshelf of popular attacks on the low-fat-diet-heart idea it is pretty remarkable that there is only one defense. Daniel Steinberg’s Cholesterol Wars. The Skeptics vs. The Preponderance of Evidence is probably more accurately called a witness for the prosecution since low-fat, in some way or other is still the law of the land.

The Skeptics vs. the Preponderance of Evidence

The book is very informative, if biased, and it provides an historical perspective describing the difficulty of establishing the cholesterol hypothesis. Oddly, though, it still appears to be very defensive for a witness for the prosecution. In any case, Steinberg introduces into evidence the Oslo Diet-Heart Study [2] with a serious complaint:

“Here was a carefully conducted study reported in 1966 with a statistically significant reduction in reinfarction [recurrence of heart attack] rate. Why did it not receive the attention it deserved?”

“The key element,” he says, “was a sharp reduction in saturated fat and cholesterol intake and an increase in polyunsaturated fat intake. In fact. each experimental subject had to consume a pint of soybean oil every week, adding it to salad dressing or using it in cooking or, if necessary, just gulping it down!”

Whatever it deserved, the Oslo Diet-Heart Study did receive a good deal of attention. The Women’s Health Initiative (WHI), liked it. The WHI was the most expensive failure to date. It found that “over a mean of 8.1 years, a dietary intervention that reduced total fat intake and increased intakes of vegetables, fruits, and grains did not significantly reduce the risk of CHD, stroke, or CVD in postmenopausal women.” [3]

The WHI, adopted a “win a few, lose a few” attitude, comparing its results to the literature, where some studies showed an effect of reducing dietary fat and some did not — this made me wonder: if the case is so clear, whey are there any failures. Anyway, it cited the Oslo Diet-Heart Study as one of the winners and attributed the outcome to the substantial lowering of plasma cholesterol.

So, “cross-examination” would tell us why, if “a statistically significant reduction in reinfarction rate” it did “not receive the attention it deserved?”

First, the effect of diet on cholesterol over five years:

The results look good although, since all the numbers are considered fairly high, and since the range of values is not shown, it is hard to tell just how impressive the results really are. But we will stipulate that you can lower cholesterol on a low-fat diet. But what about the payoff? What about the outcomes?

The results are shown in Table 5 of the original paper: Steinberg described how in the first 5 years: “58 patients of the 206 in the control group (28%) had a second heart attack” (first 3 lines under first line of blue-highlighting) but only

“… 32 of the 206 in the diet (16%)…” which does sound pretty good.

In the end, though, it’s really the total deaths from cardiac disease. The second blue-highlighted line in Table 5 shows the two final outcome. How should we compare these.

1. The odds ratio or relative risk is just the ratio of the two outcomes (since there are the same number of subjects) = CHD mortality (diet)/ CHD mortality control) = 94/79 = 1.19. This seems strikingly close to 1.0, that is, flip of a coin. These days the media, or the report itself, would report that there was a 19 % reduction in total CHD mortality.

2, If you look at the absolute values, however, the mortality in the controls is 94/206 = 45.6 % but the diet group had reduced this to 79/206 = 38.3 % so the change in absolute risk is 45.6 % – 38.3 % or only 7.3 % which is less impressive but still not too bad.

3. So for every 206 people, we save 94-79 = 15 lives, or dividing 206/15 = 14 people needed to treat to save one life. (Usually abbreviated NNT). That doesn’t sound too bad. Not penicillin but could be beneficial. I think…

Smoke and mirrors.

It’s what comes next that is so distressing. Table 10 pools the two groups, the diet and the control group and now compares the effect of smoking: on the whole population, the ratio of CHD deaths in smokers vs non-smokers is 119/54 = 2.2 (magenta highlight) which is somewhat more impressive than the 1.19 effect we just saw. Now,

1. The absolute difference in risk is (119-54)/206 = 31.6 % which sounds like a meaningful number.

2. The number needed to treat is 206/64 = 3.17 or only about 3 people need to quit smoking to see one less death

In fact, in some sense, the Oslo Diet-Heart Study provides smoking-CHD risk as an example of a meaningful association that one can take seriously. If only such a significant change had actually been found for the diet effect.

So what do the authors make of this? Their conclusion is that “When combining data from both groups, a three-fold greater CHD mortality rate is demonstrable among the hypercholesterolemic, hypertensive smokers than among those in whom these factors were low or absent.” Clever but sneaky. The “hypercholesterolemic, hypertensive” part is irrelevant since you combined the groups. In other words, what started out as a diet study has become a “lifestyle study.” They might has well have said “When combining data from fish and birds a significant number of wings were evident.” Members of the jury are shaking their heads.

Logistic regression. What is it? Can it help?

So they have mixed up smoking and diet. Isn’t there a way to tell which was more important? Well, of course, there are several ways. By coincidence, while I was writing this post, April Smith posted on facebook, the following challenge “The first person to explain logistic regression to me wins admission to SUNY Downstate Medical School!” I won although I am already at Downstate. Logistic regression is, in fact, a statistical method that asks what the relative contribution of different inputs would have to be to fit the outcome and this could have been done but in this case, I would use my favorite statistical method, the Eyeball Test. Looking at the data in Tables 5 and 10 for CHD deaths, you can see immediately what’s going on. Smoking is a bigger risk than diet.

If you really want a number, we calculated relative risk above. Again, we found for mortality, CHD (diet)/ CHD (control) = 94/79 = 1.19. But what happens if you took up smoking: Figure 10 shows that your chance of dying of heart disease would be increased by 119/54 = 2.2 or more than twice the risk. Bottom line: you decided to add saturated fat to your diet, your risk would be 1.19 what it was before which might be a chance you could take faced with authentic Foie Gras.

Daniel Steinberg’s question:

“Here was a carefully conducted study reported in 1966 with a statistically significant reduction in reinfarction rate. Why did it not receive the attention it deserved?”

Well, it did. This is not the first critique. Uffe Ravnskov described how the confusion of smoking and diet led to a new Oslo Trial which reductions in both were specifically recommended and, again, outcomes made diet look bad [4]. Ravnskov gave it the attention it deserved. But what about researchers writing in the scientific literature. Why do they not give the study the attention it deserves. Why do they not point out its status as a classic case of a saturated fat risk study with no null hypothesis. It certainly deserves attention for its devious style. Of course, putting that in print would guarantee that your grant is never funded and your papers will be hard to publish. So, why do researchers not give the Oslo-Diet-Heart study the attention it deserves? Good question, Dan.

Bibliography

1. Steinberg D: The cholesterol wars : the skeptics vs. the preponderance of evidence, 1st edn. San Diego, Calif.: Academic Press; 2007.

2. Leren P: The Oslo diet-heart study. Eleven-year report. Circulation 1970, 42(5):935-942.

3. Howard BV, Van Horn L, Hsia J, Manson JE, Stefanick ML, Wassertheil-Smoller S, Kuller LH, LaCroix AZ, Langer RD, Lasser NL et al: Low-fat dietary pattern and risk of cardiovascular disease: the Women’s Health Initiative Randomized Controlled Dietary Modification Trial. JAMA 2006, 295(6):655-666.

4. Ravnskov U: The Cholesterol Myths: Exposing the Fallacy that Cholesterol and Saturated Fat Cause Heart Disease. Washington, DC: NewTrends Publishing, Inc.; 2000.

Red Meat and the New Puritans

Posted: April 7, 2011 in Association and Causality, Protein, The Nutrition Story
Tags: Barry Popkin, beef, Dr. R Sinha, hazard ratio, Meat Intake and Mortality, mortality, red meat,, statistics

“Dost thou think, because thou art virtuous, there shall be no more cakes and ale?”

— William Shakespeare, Twelfth Night.

Experts on nutrition are like experts on sexuality. No matter how professional they are in general, in some way they are always trying to justify their own lifestyle. They share a tendency to think that their own lifestyle is the one that everybody else should follow and they are always eager to save us from our own sins, sexual or dietary. The new puritans want to save us from red meat. It is unknown whether Michael Pollan’s In Defense of Food was reporting the news or making the news but it’s coupling of not eating too much and not eating meat is common. More magazine’s take on saturated fat was very sympathetic to my own point of view and I probably shouldn’t complain that tacked on at the end was the conclusion that “most physicians will probably wait for more research before giving you carte blanche to order juicy porterhouse steaks.” I’m not sure that my physician knows about the research that already exists or that I am waiting for his permission on a zaftig steak.

“Daily Red Meat Raises Chances Of Dying Early” was the headline in the Washington Post last year. This scary story was accompanied by the photo below. The gloved hand slicing roast beef with a scalpel-like instrument was probably intended to evoke CSI autopsy scenes, although, to me, the beef still looked pretty good if slightly over-cooked. I don’t know the reporter, Rob Stein, but I can’t help feeling that we’re not talking Woodward and Bernstein here. For those too young to remember Watergate, the reporters from the Post were encouraged to “follow the money” by Deep Throat, their anonymous whistle-blower. A similar character, claiming to be an insider and identifying himself or herself as “Fat Throat,” has been sending intermittent emails to bloggers, suggesting that they “follow the data.”

The Post story was based on a research report “Meat Intake and Mortality” published in the medical journal, Archives of Internal Medicine by Sinha and coauthors. It got a lot of press and had some influence and recently re-surfaced in the Harvard Men’s Health Watch in a two part article called, incredibly enough, “Meat or beans: What will you have?” (The Health Watch does admit that “red meat is a good source of iron and protein and…beans can trigger intestinal gas” and that they are “very different foods”) but somehow it is assumed that we can substitute one for the other.

Let me focus on Dr. Sinha’s article and try to explain what it really says. My conclusion will be that there is no reason to think that any danger of red meat has been demonstrated and I will try to point out some general ways in which one can deal with these kinds of reports of scientific information.

A few points to remember first. During the forty years that we describe as the obesity and diabetes epidemic, protein intake has been relatively constant; almost all of the increase in calories has been due to an increase in carbohydrates; fat, if anything, went down. During this period, consumption of almost everything increased. Wheat and corn, of course went up. So did fruits and vegetables and beans. The two things whose consumption went down were red meat and eggs. In other words there is some a priori reason to think that red meat is not a health risk and that the burden of proof should be on demonstrating harm. Looking ahead, the paper, like analysis of the population data, will rely entirely on associations.

The conclusion of the study was that “Red and processed meat intakes were associated with modest increases in total mortality, cancer mortality, and cardiovascular disease mortality.” Now, modest increase in mortality is a fairly big step down from “Dying Early,” and surely a step-down from the editorial quoted in the Washington Post. Written by Barry Popkin, professor of global nutrition at the University of North Carolina it said: “This is a slam-dunk to say that, ‘Yes, indeed, if people want to be healthy and live longer, consume less red and processed meat.'” Now, I thought that the phrase “slam-dunk” was pretty much out after George Tenet, then head of the CIA, told President Bush that the Weapons of Mass Destruction in Iraq was a slam-dunk. (I found an interview with Tenet after his resignation quite disturbing; when the director of the CIA can’t lie convincingly, we are in big trouble). And quoting Barry Popkin is like getting a second opinion from a member of the “administration.” It’s definitely different from investigative reporting like, you know, reading the article.

So what does the research article really say? As I mentioned in my blog on eggs, when I read a scientific paper, I look for the pictures. The figures in a scientific paper usually make clear to the reader what is going on — that is the goal of scientific communication. But there are no figures. With no figures, Dr. Sinha’s research paper has to be analyzed for what it does have: a lot of statistics. Many scientists share Mark Twain’s suspicion of statistics, so it is important to understand how it is applied. A good statistics book will have an introduction that says something like “what we do in statistics, is try to put a number on our intuition.” In other words, it is not really, by itself, science. It is, or should be, a tool for the experimenter’s use. The problem is that many authors of papers in the medical literature allow statistics to become their master rather than their servant: numbers are plugged into a statistical program and the results are interpreted in a cut-and-dried fashion with no intervention of insight or common sense. On the other hand, many medical researchers see this as an impartial approach. So let it be with Sinha.

What were the outcomes? The study population of 322, 263 men and 223, 390 women was broken up into five groups (quintiles) according to meat consumption, the highest taking in about 7 times as much as the lower group (big differences). The Harvard News Letter says that the men who ate the most red meat had a 31 % higher death rate than the men who ate the least meat. This sounds serious but does it tell you what you want to know? In the media, scientific results are almost universally reported this way but it is entirely misleading. (Bob has 30 % more money than Alice but they may both be on welfare). To be fair, the Abstract of the paper itself reported this as a hazard ratio of 1.31 which, while still misleading, is less prejudicial. Hazard ratio is a little bit complicated but, in the end, it is similar to odds ratio or risk ratio which is pretty much what you think: an odds ratio of 2 means you’re twice as likely to win with one strategy as compared to the other. A moment’s thought tells you that this is not good information because you can get an odds ratio of 2, that is, you can double your chances of winning the lottery, by buying two tickets instead of one. You need to know the actual odds of each strategy. Taking the ratio hides information. Do reporters not know this? Some have told me they do but that their editors are trying to gain market share and don’t care. Let me explain it in detail. If you already understand, you can skip the next paragraph.

A trip to Las Vegas

Taking the hazard ratio as more or less the same as odds ratio or risk ratio, let’s consider applying odds (in the current case, they are very similar). So, we are in Las Vegas and it turns out that there are two black-jack tables and, for some reason (different number of decks or something), the odds are different at the two tables (odds are ways of winning divided by ways of not winning). Table 1 pays out on average once every 100 hands. Table 2 pays out once in 67 hands. The odds are 1/99 or close to one in a hundred at the first table and 1/66 at the second. The odds ratio is, obviously the ratio of the two odds or 1/66 divided by 1/99 or about 1.55. (The odds ratio would be 1 if there were no difference between the two tables).

Right off, something is wrong: if you were just given the odds ratio you would have lost some important information. The odds ratio tells you that one gambling table is definitely better than the other but you need additional information to find out that the odds aren’t particularly good at either table: technically, information about the absolute risk was lost.

So knowing the odds ratio by itself is not much help. But since we know the absolute risk of each table, does that help you decide which table to play? Well, it depends who you are. For the guy who is at the blackjack table when you go up to your hotel room to go to sleep and who is still sitting there when you come down for the breakfast buffet, things are going to be much better off at the second table. He will play hundreds of hands and the better odds ratio of 1.5 will pay off in the long run. Suppose, however, that you are somebody who will take the advice of my cousin the statistician who says to just go and play one hand for the fun of it, just to see if the universe really loves you (that’s what gamblers are really trying to find out). You’re going to play the hand and then, win or lose, you are going to go do something else. Does it matter which table you play at? Obviously it doesn’t. The odds ratio doesn’t tell you anything useful because you know that your chances of winning are pretty slim either way.

Now going over to the Red Meat article the hazard ratio (again, roughly the odds ratio) between high and low red meat intakes for all-cause mortality for men, for example, is 1.31 or, as they like to report in the media 31 % higher risk of dying which sounds pretty scary. But what is the absolute risk? To find that we have to find the actual number of people who died in the high red meat quintile and the low end quintile. This is easy for the low end: 6,437 people died from the group of 64,452, so the probability (probability is ways of winning divided by total possibilities) of dying are 6,437/64,452 or just about 0.10 or 10 %. It’s a little trickier for the high red meat consumers. There, 13,350 died. Again, dividing that by the number in that group, we find an absolute risk of 0.21 or 21 % which seems pretty high and the absolute difference in risk is an increase of 10 % which still seems pretty significant. Or is it? In these kinds of studies, you have to ask about confounders, variables that might bias the results. Well, here, it is not hard to find. Table 1 reveals that the high red meat group had 3 times the number of smokers. (Not 31 % more but 3 times more). So the authors corrected the data for this and other effects (education, family history of cancer, BMI, etc.) which is how the final a value of 1.31 was obtained. Since we know the absolute value of risk in the lowest red meat group, 0.1 we can calculate the risk in the highest red meat group which will be 0.131. The absolute increase in risk from eating red meat, a lot more red meat, is then 0.131 – 0.10 = 0.031 or 3.1 % which is quite a bit less than we thought.

Now, we can see that the odds ratio of 1.31 is not telling us much — and remember this is for big changes, like 6 or 7 times as much meat; doubling red meat intake (quintiles 1 and 2) leads to a hazard ratio of 1.07. What is a meaningful odds ratio? For comparison, the odds ratio for smoking vs not smoking for incidence of lung disease is about 22.

Well, 3.1 % is not much but it’s something. Are we sure? Remember that this is a statistical outcome and that means that some people in the high red meat group had lower risk, not higher risk. In other words, this is what is called statistically two-tailed, that is, the statistics reflect changes that go both ways. What is the danger in reducing meat intake. The data don’t really tell you that. Unlike cigarettes, where there is little reason to believe that anybody’s lungs really benefit from cigarette smoke (and the statistics are due to random variation), we know that there are many benefits to protein especially if it replaces carbohydrate in the diet, that is, the variation may be telling us something real. With odds ratios around 1.31 — again, a value of 1 means that there is no difference — you are almost as likely to benefit from adding red meat as you are reducing it. The odds still favor things getting worse but it really is a risk in both directions. You are at the gaming tables. You don’t get your chips back. If reducing red meat does not reduce your risk, it may increase it. So much for the slam dunk.

What about public health? Many people would say that for a single person, red meat might not make a difference but if the population reduced meat by half, we would save thousands of lives. The authors do want to do this. At this point, before you and your family take part in a big experiment to save health statistics in the country, you have to ask how strong the relations are. To understand the quality of the data, you must look for things that would not be expected to have a correlation. “There was an increased risk associated with death from injuries and sudden death with higher consumption of red meat in men but not in women.” The authors dismiss this because the numbers were smaller (343 deaths) but the whole study is about small differences and it sounds like we are dealing with a good deal of randomness. Finally, the authors set out from the start to investigate red meat. To be fair, they also studied white meat which was slightly beneficial. But what are we to compare the meat results to? Why red meat? What about potatoes? Cupcakes? Breakfast cereal? Are these completely neutral? If we ran these through the same computer, what would we see? And finally there is the elephant in the room: carbohydrate. Basic biochemistry suggests that a roast beef sandwich may have a different effect than roast beef in a lettuce wrap.

So I’ve given you the perspective of a biochemistry professor. This was a single paper and surely not the worst, but I think it’s not really about science. It’s about sin.

Nutrition & Metabolism Society

Richard David Feinman

Click to follow this blog.

Recent Posts

Blogroll

Archives

Posts Tagged ‘statistics’

Red meat and cancer

Observations Generate hypotheses. Observational Studies Test Hypotheses. Association Implies Causality (Sometimes).

Uses and misuses of group statistics. Bill Gates walks into a bar…

Flawed studies II. Occam’s Razor and How to Reduce Fructose Consumption.

Reading the Scientific Literature. A Guide to Flawed Studies.

Making Americans Afraid of Meat.

Intention-to-treat II: Foster, et al: Weight and Metabolic Outcomes After 2 Years

Nothing wrong with Observational Studies. And Association does Imply Causality but…

Evidence Based Medicine and Admissibility. IV. The Oslo Diet-Heart Study.

Red Meat and the New Puritans

Click to follow this blog.

Recent Posts

Categories

Blogroll

Archives

Posts Tagged ‘statistics’

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this: