Richard David Feinman

Following up from chapters in The World Turned Upside Down, I will try to provide a guide to getting through the medical literature. I will talk about relative risk first with an excerpt from the book and a quick way to get a feel for what relative risk really is.

It has been frequently pointed out that to succeed at major league baseball all you have to do is screw up no more than 70 % of the time. In fact ,it is almost 75 years since someone was able to come up with a failure rate as low as 60 %. (Ted Williams hit .406 in 1941). The point is that statistics is about interpretation. It is how you describe things. As in Paulos’s Once Upon a Number, mathematics and especially statistics is a story, and how you tell it.  The potential for being misled is obviously great. The idea that statistics is a cut-and-dried standard set of manipulations into which you pour your data and from which you are automatically given significance, importance and truth, is one of the major components in the failure of the medical nutrition literature.

The particular statistical methods that you use, or whether you use any at all should depend on the story and that of course depends on the question that you are asking. A scientific study may be a “documentary” in which the data speak for themselves but even if a complicated analysis is carried out, we should be confident that we know what was in the original data. Nowhere is this more important than the misuse of relative risk. The story in the numerous epidemiologic studies in the medical literature frequently come up with relative risks of something like 1.4. What does that mean? Well, one way of describing it is that you have a 40 % greater chance of getting the disease if you eat red meat instead of white meat, or white rice instead of brown rice, or anything instead of blueberries. Forty per cent sounds serious. But there are a lot of reasons why it might not mean anything at all.  I will describe the problem first with an excerpt from The World Turned Upside Down. Then I’ll give you a quick way of seeing what you’re up against with relative risk.

You in Las Vegas

“You are in Las Vegas. There are two black‑jack tables and, for some reason (different number of decks or something), they have different probabilities of paying out. The probability of winning at Table One is 1 in 100 hands, or 0.01 or 1 %. At Table Two, the probability of winning is 1 in 80 or about 1.27%. The ratio of the probabilities is 1.27/1.0 = 1.27. (A ratio of 1 would mean that there is no difference between the tables). Right off, something is wrong: you lost a lot of information. One gambling table is definitely better than the other but the odds aren’t particularly good at either table. But you had to know that in advance; you can’t tell from the probability ratio because the information about the real payoff is lost. Suppose, however, that you did get a glimpse at the real info and you could find out what the absolute odds are at the different tables: 1 % at Table One, 1.27 % at Table Two. Does that help? Well, it depends on who you are. For the guy who is sitting at the black‑jack table when you go up to sleep in your room at the hotel, and who is still there when you come down for the breakfast buffet, things are going to be much better off at the second table. He will play hundreds of hands and the better odds ratio of 1.27 is likely to pay off. Suppose, however, that you are somebody who will take the advice of my cousin, the statistician, who says to just go and play one hand for the fun of it, just to see if the universe loves you (that’s what gamblers are really trying to find out). You’re going to play the hand and then, win or lose, you are going to do something else. Does it matter which table you play at? Obviously it doesn’t. The odds ratio doesn’t tell you anything useful because your chances of winning are pretty slim either way. Put another way, if you buy two lottery tickets instead of one, your chances of winning are doubled, but does that make you want to play?”

What are the Odds?

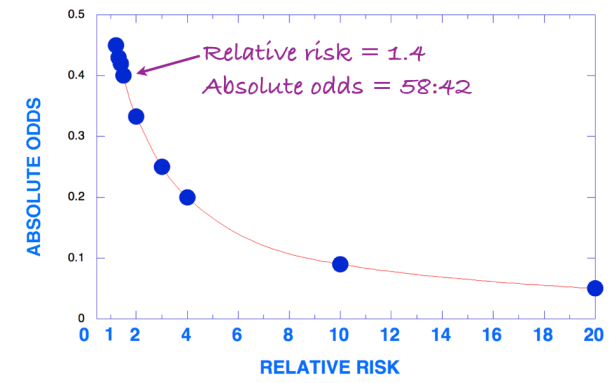
Here’s a good way to get a sense of the low relative risk that you see in the literature. If the relative risk is 1.4, then some unknown number of patients x will come down with the disease in the intervention group, say. The control group, however, will have 1.4x cases. The total population of each group is usually chosen to be almost the same, so the fraction of treated patients that have disease = x/(x + 1.4 x) = x/2.4x = 1/2.4 = 42 %. The control group will have a 58%.  The difference is 16 %, clearly less scary than 40 % but, more important, you have to ask yourself what the disease is and whether the people in the intervention group were really not-responders or were really people who got sick from the intervention. This is another way of looking at the data. In essence, you are looking at the population of people who got sick and asking what are the odds that they were in the intervention group. The standard for asking what would be serious risk is still cigarette smoking and lung cancer where the relative risk is 20 or odds of 95:1.

Anyway, if you like this method of eye balling relative risk, you can calculate fraction of success as 1/(1+RR) which is shown in the figure. Even at 2:1 odds, the intervention folks are still batting .333 which is pretty good (that is, bad) for the major leagues.

Extra: note on Language of Odds and Risk

Risk and odds are not exactly the same thing although, to keep it simple, I didn’t distinguish between. However, to be precise:

Probability of an event happening = number of particular events/number of total events. If 5 people in a population of 100 have diabetes, the probability, p = 5/100 = 0.05 or “about 5 per hundred,” or “about 1 in 20.”

Odds of an events = number of times event happens / number times doesn’t happen. For example, the odds of 5 people in 100 having diabetes = 5/ (100-5) = 5/95 = 0.053 or “ about 1 to 5,” or, as the bookies say, “about 19 to 1 against.” As the number of events becomes smaller, the probability and the odds are pretty much the same and to get a feel for things,

Risk, in simplest form, is the probability. Relative risk is the ratio. If the risk of disease is 5 per 100 (5 %) and after consuming some macronutrient of importance, the risk is 6 per hundred (6 %), the relative risk would be (6/100)/5/100) = 6:5 = 1.2 or 20 % increase in risk.

The Major caveat, however, is that if the risks at baseline and risk with the dietary intake were 5/10,000 (0.06 %) and 5/10, 000 (0.05 %), the relative risk would still be 1.2 or 20 % which looks good in the Abstract of the paper but doesn’t sound important when you know that the absolute values is a difference of one hundredth of 1 %.  That’s why you should ask for the raw data.